Leetcode in Java - 46. Permutations (backtracking)

 

 

backtracking이란?

backtrack은 `후퇴`로 번역되는데, 미로에서 길을 찾을 때와 같이 막다른 길에 도달하면 마지막 선택으로 돌아가는 것을 말한다.

 

 

backtracking과 다른 알고리즘의 구별

모든 가능성을 전부 탐색해야 하는 brute force 방식으로, 각 탐색이 다른 탐색에 영향을 미치지 않으므로 DP와 다르고, 각 후보(candidate)는 다른 후보와 더 낫거나 모자라지 않으므로, 전역 최댓값을 구하기 위해 국소적 최솟값을 선택하는 greedy와도 구별된다. 

 

 

backtracking 전체적인 흐름

출처 : https://www.geeksforgeeks.org/introduction-to-backtracking-2/

 

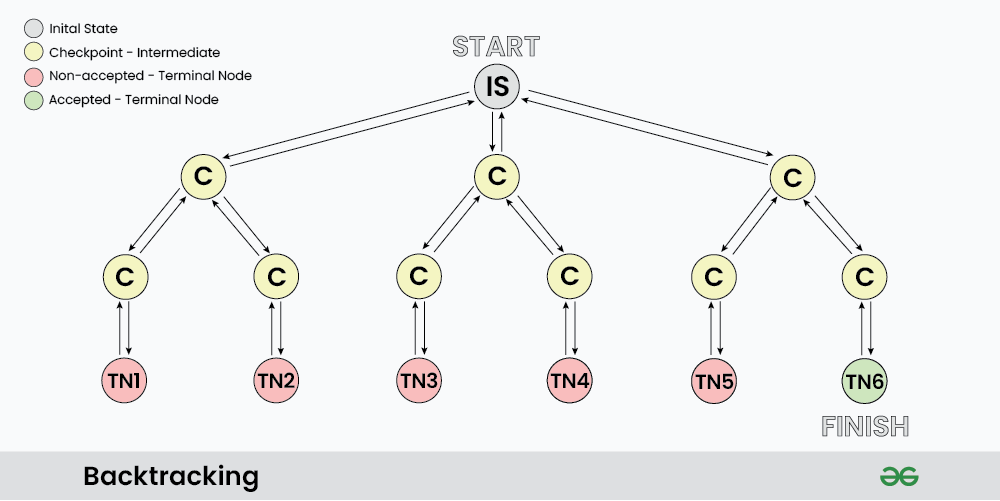
backtracking은 모든 가능한 경우의 수를 탐색하여 최종 답안인 집합 S를 구하게 된다. 후보인 s가 S에 포함될지 안될지를 판단후 포함되면 S에 추가하고, 포함되지 않으면 후퇴해서 다른 s를 찾는다.

 

 

코드

/**
 * T.C
 * = {backtrack 1회의 시간복잡도} * {backtrack 횟수}
 * = {n} * {n!}
 * = O(n*n!)
 *
 * S.C
 * = {각 순열의 길이} * {순열의 갯수}
 * = {n} * {n!}
 * = O(n*n!)
 */
 
class SolutionBacktracking {
    public List<List<Integer>> permute(int[] nums) {
        List<List<Integer>> ans = new ArrayList<List<Integer>>();
        backtrack(ans, new ArrayList<>(), nums);
        return ans;
    }

    public void backtrack(List<List<Integer>> ans, List<Integer> tempList, int[] arr) {
        int n = arr.length;

        if (tempList.size() == n) {
            ans.add(new ArrayList<>(tempList));
        } else {
            for (int i=0; i<n; i++) {
                int k = arr[i];
                if (tempList.contains(k)) continue;
                tempList.add(k);
                backtrack(ans, tempList, arr);
                tempList.remove(tempList.size()-1);
            }
        }
    }

    /**
     i  tempList          ans
     x  []                []
     0  [1]               []
     0  [1,2]             []
     1  [1,2]             []
     0  [1,2]             []
     1  [1,2]             []
     2  [1,2,3]           []
     x  [1,2,3]           [[1,2,3]]
     2  [1,3]             [[1,2,3]]
     0  [1,3]             [[1,2,3]]
     1  [1,3,2]           [[1,2,3]]
     x  [1,3,2]           [[1,2,3], [1,3,2]]
     2  [1,3]             [[1,2,3], [1,3,2]]
     1  [2]               [[1,2,3], [1,3,2]]
     0  [2,1]             [[1,2,3], [1,3,2]]
     0  [2,1]             [[1,2,3], [1,3,2]]
     1  [2,1]             [[1,2,3], [1,3,2]]
     2  [2,1,3]           [[1,2,3], [1,3,2]]
     x  [2,1,3]           [[1,2,3], [1,3,2], [2,1,3]]
     1  [2]               [[1,2,3], [1,3,2], [2,1,3]]
     2  [2,3]             [[1,2,3], [1,3,2], [2,1,3]]
     0  [2,3,1]           [[1,2,3], [1,3,2], [2,1,3]]
     x  [2,3,1]           [[1,2,3], [1,3,2], [2,1,3], [2,3,1]]
     1  [2,3]             [[1,2,3], [1,3,2], [2,1,3], [2,3,1]]
     2  [2,3]             [[1,2,3], [1,3,2], [2,1,3], [2,3,1]]
     2  [3]               [[1,2,3], [1,3,2], [2,1,3], [2,3,1]]
     0  [3,1]             [[1,2,3], [1,3,2], [2,1,3], [2,3,1]]
     0  [3,1]             [[1,2,3], [1,3,2], [2,1,3], [2,3,1]]
     1  [3,1,2]           [[1,2,3], [1,3,2], [2,1,3], [2,3,1]]
     x  [3,1,2]           [[1,2,3], [1,3,2], [2,1,3], [2,3,1], [3,1,2]]
     1  [3,2]             [[1,2,3], [1,3,2], [2,1,3], [2,3,1], [3,1,2]]
     0  [3,2,1]           [[1,2,3], [1,3,2], [2,1,3], [2,3,1], [3,1,2]]
     x  [3,2,1]           [[1,2,3], [1,3,2], [2,1,3], [2,3,1], [3,1,2], [3,2,1]]
     1  [3,2,1]           [[1,2,3], [1,3,2], [2,1,3], [2,3,1], [3,1,2], [3,2,1]]
     2  [3,2,1]           [[1,2,3], [1,3,2], [2,1,3], [2,3,1], [3,1,2], [3,2,1]]
     2  [3]               [[1,2,3], [1,3,2], [2,1,3], [2,3,1], [3,1,2], [3,2,1]]

     */
}

 

 

 

---

 

 

 

참고 자료

 

• LeetCode 46. Permutations
• GeeksforGeeks "Introduction to Backtracking"